notes

In here are the list of things I did for a particular hour or day. Also included here are the screenshots of games I played, or videos I watched or listened to, or just random things I stumbled upon. I'll occasionally write down what I'm thinking, or things I'm planning to do.

[ 2024-02-15 ]

20:09 [link] [context] #site

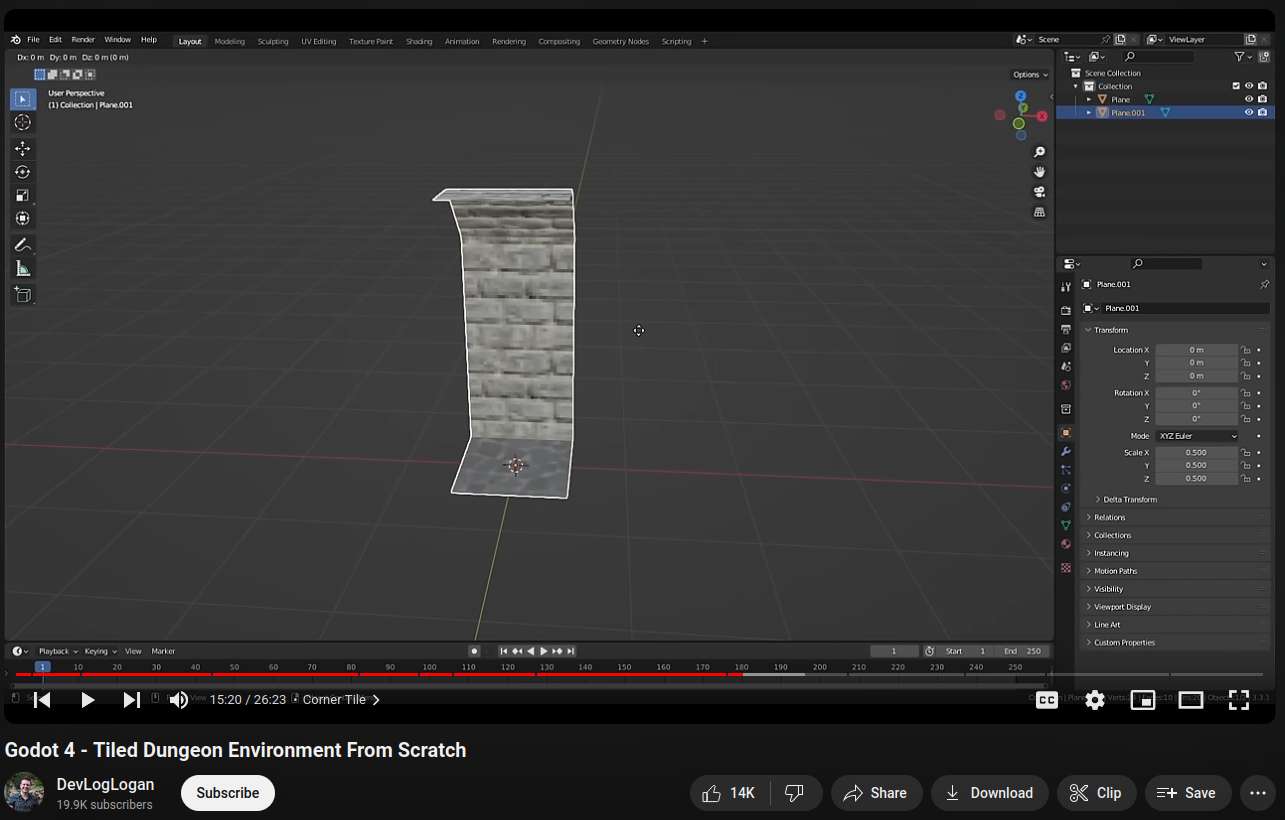
Added some markdown library, so my logs would look well formatted. The markdown library is actually using the older spec, so triple ``` isn't event supported. It's good enough for now, but ideally, I should just avoid markdown and just put longer notes on a separate lua page.

I also gave myself a haircut today. By haircut, I mean I trimmed excess hair so the hair would stop poking my eyes, and I could save some soap and shampoo. Cutting my own hair saved me about $2, and importantly saves me the anxiety of having to go outside. Needless to say, my hair looks like shit, before and after.

But as the saying goes, even stinkiest fart eventually goes away. I'm sure in the whole history of mankind someone said that, surely. I just remembered a certain shark saying "fart in the wind", which is identical in meaning.

🕒 15:13

🕒 15:12

🕛 12:15

🕛 12:08

11:23 [link] [context] #math

I skimmed over the book of abstract algebra last night, I didn't find anything I could use.

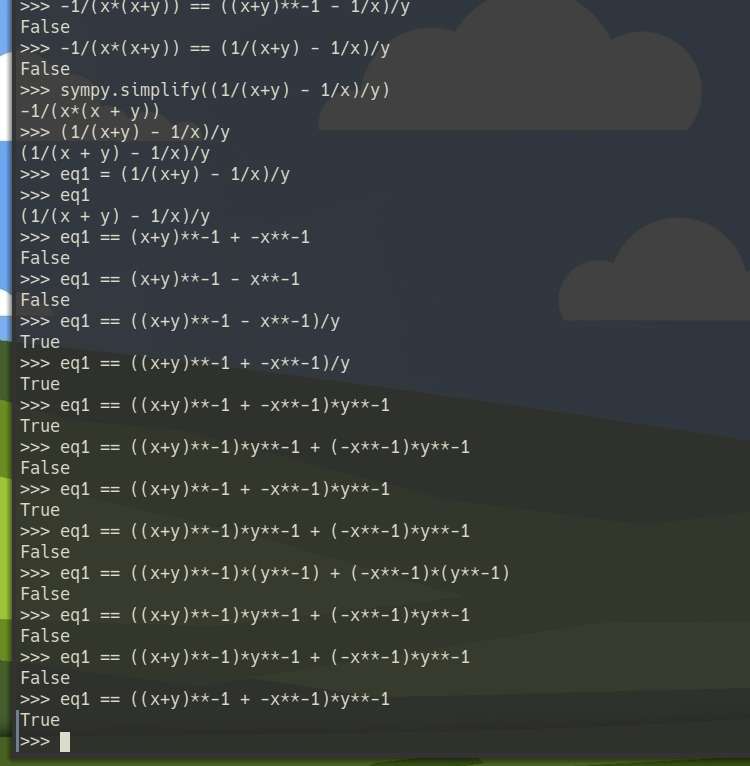
Played around more with equations, on paper, vim, and with python/sympy.

What I just realized is that, 1/(x+y) - 1/x can no longer be simplified. The book actually does simplification with (1/(x+y) - 1/x)/y

Second realization is that sympy does not automatically simplify when comparing equality between expressions. I seriously started questioning and doubting myself when it returns false with (a*b)*x == a*x + b*x.

I actually need to do simplify((a*b)*x) == simplify(a*x + b*x)

That said, the furthest simplification I got was

   (1/(x+y) - 1/x)/y
 = (x+y)^-1*(y^-1) + (-x^-1)*(y^-1)

^-1 looks really messy though, for I'll use ~ as an abbreviation for ^-1

   (1/(x+y) - 1/x)/y
 = (x+y)~y~ + -x~y~

I also found out that a~b~ = (ab)~, this is actually I learned from abstract algebra as well, but it's something I won't see when looking up exponential laws.

   (1/(x+y) - 1/x)/y
 = (x+y)~y~ + -x~y~
 = [(x+y)y]~ + (-xy)~

Alas, that's hardly a simplification. It's still quite far away from the simplification shown by the calculus book and sympy:

  (1/(x+y) - 1/x)/y
 = -1/(x*(x + y))

Just I was about to resign to my fate as a retard who can't even do basic algebra by using only exponential laws, I realized that sympy does the following (de)simplification:

   x~ + y~
 = (x + y)/(x*y)
 = (x + y)(x*y)~

Interesting, it's not immediately clear how I would do that using theorems from groups, rings, fields and whatnot. Then again, it's probably using a basic fraction rule that I'm too dumb to see. Well, at least I have a lead for the next morning session.

Ultimately, my goal is to show (to myself) that I can do algebraic manipulations without using fractions. It's a hill I'm willing to die on, probably. Or at least, lose a leg.

🕙 10:18

🕙 10:17

🕙 10:16

🕓 04:37

🕓 04:17

🕒 03:20